Part Wheel Strategy and The Mathematics
In a prior article we provided a Trifecta Part Wheel example using a key horse in the first position and introducing the mathematics for calculating the number of combinations of a Part Wheel wager, Pyramid Style. Click here to read that article. In this article we’re going to explain the mathematics when more than one horse is used in the winning position. And, we’re going to go over the math involved with a similar Superfecta Part Wheel wager.
Below is a copy of the race scenario created in the prior post for an 11-horse field.
| Horse | Odds | Thoughts |
|---|---|---|
| 1 | 2-1 | Your top selection, with high marks on Class, Distance, Form, and Pace. |
| 2 | 5-1 | Up and coming horse, improving with every start, but not quite up to the level of #1 yet. |
| 4 | 8-1 | Horse with past ability, off for 6-months, and workouts are solid. |
| 6 | 12-1 | Trainer statistics for this type of race show good percentage of horses hitting the board, but low win%. |
| 9 | 20-1 | Horse that rarely wins, but manages to finish 3rd from time-to-time at double digit odds. |
| 11 | 40-1 | Beyer Figs are well below the contenders, but with some improvement maybe good enough to hit the board. |
Upon further reflection, we decide that #2 (with a little improvement) has a shot at winning this race. So, now instead of keying only #1 in the win spot, we decide to include both #1 and #2 in the win spot. We also decide that their are only four horses (1,2,4,6) that are good enough to challenge for the top two spots. Given those assumptions, our new Part Wheel looks like this:
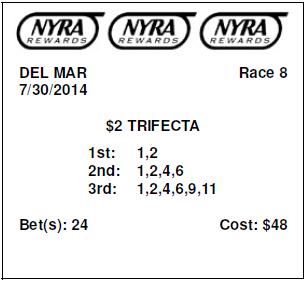
$2 Trifecta, Part Wheel, {1,2} with {1,2,4,6} with {1,2,4,6,9,11}.
This results in 24 combinations. These combinations will not print out on your ticket, but they are implied by the Part-Wheel wager. Below is an example of what your ticket might look like.
So, how did we compute the 24 combinations? If your wager is constructed in a way where you are adding horses to each “leg” of the wager (we refer to that as Pyramid Style) the math is as follows:
Presume a Trifecta Part Wheel wager of: {A} with {B} with {C}.
Where {A} is the number of horses in the 1st position, {B} is the number of horses in the 2nd position, and {C} is the number of horses in the 3rd position.
Total Combinations = A x (B-1) x (C-2)
Here are some examples:
| Part Wheel Trifecta Wager | Math:A x (B-1) x (C-2) | Combinations | Cost (Presuming $2 wagers) |
|---|---|---|---|
| 1,2 with 1,2,4,6 with 1,2,4,6,9,11 | 2 x 3 x 4 | 24 | $48 |
| 1,2 with 1,2,4,6,9,11 with 1,2,4,6,9,11 | 2 x 5 x 4 | 40 | $80 |
| 1,2 with 1,2,4,6 with 1,2,4,6,8,9,11 | 2 x 3 x 5 | 30 | $60 |
| 1,2 with 1,2,4 with 1,2,4,6,8,9,11 | 2 x 2 x 5 | 20 | $40 |
Now, before you get too scared off by the total dollars required for some of these wagers, remember this example was based on a $2 wager. Almost all tracks allow a minimum wager on Trifecta of $1, and some as low as 50-cents. So, converting from a $2 to a 50-cent Trifecta would cut the above investments to $12, $20, $15, and $10 respectively.
Superfecta Part-Wheel Math
Superfectas (selecting the top 4 finishers) add another layer of complication to the mathematics, and of course create more combinations. However, nearly all major racetracks now offer a minimum 10-cent Superfecta wager. This can make them an attractive play even for a beginner. The following explain the mathematics involved in computing the number of combinations in a Superfecta Part Wheel (Pyramid Style):
Presume a Superfecta Part Wheel wager of: {A} with {B} with {C} with {D}
Where {A} is the number of horses in the 1st position, {B} is the number of horses in the 2nd position, {C} is the number of horses in the 3rd position, {D} is the number of horses in the 4th position.
Total Combinations = A x (B-1) x (C-2) x (D-3)
*NOTE: As with the Triple mathematics, this presumes you are adding (Pyramid Style) horses to each “leg” of the wager.
Here are some examples (presuming an 11-horse field):
| Part Wheel Superfecta Wager | Math:A x (B-1) x (C-2) x (D-3) | Combinations | Cost (Presuming 10-cent wagers) |
|---|---|---|---|
| 1,2 with 1,2,4,6,9,11 with 1,2,4,6,9,11 with 1,2,4,6,9,11 | 2 x 5 x 4 x 3 | 120 | $12.00 |
| 1,2 with 1,2,4,6 with 1,2,4,6,9,11 with ALL | 2 x 3 x 4 x 8 | 192 | $19.20 |
| 1,2,4,6 with 1,2,4,6 with 1,2,4,6,9,11 with 1,2,4,6,9,11 | 4 x 3 x 4 x 3 | 144 | $14.40 |
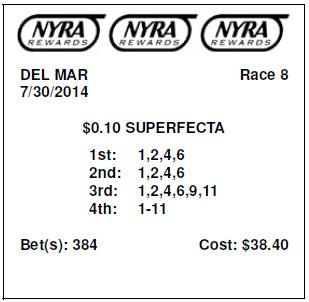
| 1,2,4,6 with 1,2,4,6 with 1,2,4,6,9,11 with ALL | 4 x 3 x 4 x 8 | 384 | $38.40 |
Each of these wagers tells a different story. In the first two, we are fairly confident that either #1 or #2 will win and we are “spreading out” to various degrees in the “lower legs” of the Superfecta wager. In the 2nd example we are using ALL horses in the 4th position.
The last two examples show confidence that the top two finishers will come from four horses (1,2,4,6) and then we spread out from there. Below is a sample of what your ticket might look like for the final example on the above list.
There are countless ways to construct Superfecta Part Wheel tickets. I highly recommend reading Steve Crist’s Book, Exotic Betting: How to make the Multihorse, Multirace Bets that Win Racing’s Biggest Payoffs for many creative ways to approach this type of wager.


Pingback: Kentucky Derby 141 Thoughts | Leap of Thought